Penningmängdstillväxtens prognosförmåga för inflationen i Sverige skattad på data över fyra århundraden
I denna artikel använder vi ett historiskt datamaterial bestående av svenska data från 1620 till 2021 för att undersöka om penningmängdstillväxt har prognosförmåga för inflation. Vi använder metoder som möjliggör formella modellval mellan olika skattade modeller. Vår inomsampelanalys indikerar ett starkt stöd för hypotesen att penningmängdstillväxt kan prognostisera inflation. Detta återspeglas dock inte i out-of-sample-analysen, där prognosprecisionen för inflationen inte förbättras när penningmängdstillväxten beaktas.
De senaste årtiondena har penningmängden i såväl forskning som praktisk penningpolitik fram till nyligen förknippats med en blygsam roll när det gäller att förklara och prognostisera inflation. Det kan noteras att Woodford (2008) drog slutsatsen att det i den nykeynesianska modellen inte finns någon stark anledning att ge penningmängden en framträdande roll och 2021 övergav Europeiska centralbanken (2021) – en av de historiskt sett starkaste förespråkarna för penningmängdsanalys – sin tvåpelarstrategi för ett ”integrerat analytiskt ramverk”. De okonventionella penningpolitiska åtgärder som centralbanker tog till under finanskrisen 2008, eurokrisen och coronapandemin har dock – tillsammans med den kraftiga uppgång i inflation som många länder upplevde 2022 till 2023 – givit nytt bränsle åt debatten kring huruvida monetära aggregat kan prediktera inflation; se t ex Berger m fl (2023) och Borio m fl (2023).
I denna artikel bidrar vi till denna debatt genom att undersöka penningmängdens prognosförmåga för inflationen i Sverige. Detta görs genom att vi skattar bivariata vektorautoregressionsmodeller (VAR-modeller) på ett datamaterial som sträcker sig från 1620 till 2021. Modellerna bygger på bayesianska metoder utvecklade av Chan och Eisenstat (2018) och tillåter tidsvariation i såväl parametrar som störningstermens varians – egenskaper som förefaller viktiga att beakta givet att den långa tidsperioden innebär en hög sannolikhet att samband kan ha förändrats. Metoderna innebär också att formell analys kring modellval kan utföras.
Genom vår analys ansluter vi oss till en liten men växande skara forskare som relativt nyligen har utfört ekonometrisk analys på mycket långa tidsserier. Bland dessa kan noteras Harvey m fl (2010) som studerade trender i råvarupriser på ett datamaterial som sträckte sig från 1650 till 2005. Golez och Koudjis (2018) samt Verdickt m fl (2019) analyserade huruvida det gick att prognostisera aktieavkastningar på datamaterial som sträckte sig fyra århundraden respektive 165 år. En studie som i vissa hänseenden ligger nära vår är Plakandaras m fl (2023) som analyserade realräntor under 700 år med hjälp av VAR-modeller med tidsvarierande parametrar.1
Återstående del av denna artikel är upplagd på följande sätt: I avsnitt 1 beskriver vi data och i avsnitt 2 presenteras det metodologiska ramverk som den empiriska analysen baseras på. Resultaten redovisas i avsnitt 3 och artikeln avslutas i avsnitt 4 med en kortfattad diskussion.
- Data
I vår analys används tidsserier på penningmängd och priser som sträcker sig från 1620 till 2021. Penningmängdsserien motsvarar M3 och ges av Edvinsson och Ögrens (2014) data mellan 1620 och 2012. Dessa kompletteras med data från SCB för åren 2013 till 2021. Beträffande priser så mäts dessa med konsumentprisindex (KPI) publicerat av SCB från 1914 till 2021. För perioden före 1914 används KPI beräknat av Edvinsson och Söderberg (2010, 2011). För detaljer rörande data, se Edvinsson m fl (2025) samt ovan nämnda källor.
Analysen baseras på årliga procentuella förändringar av variablerna, dvs vi modellerar penningmängdstillväxt och inflation. Tidsserierna återges i figur 1.
Den studerade perioden är mycket lång och består av ett antal olika regimer. För att studera dessa närmare delar vi in perioden i följande fyra delperioder: 1) Koppar- och silverstandard 1624 till 1776, 2) silverstandard 1777 till 1873, 3) guldstandard 1873 till 1971 och 4) post-Bretton Woods-systemet som följt därefter. Det bör dock noteras att dessa delperioder inte bör ses som inbördes stabila. Ett flertal relevanta händelser indikerar att regimerna hade variation inom sig, såsom kopparmyntens kraftiga värdefall 1626–28, massutgivning av kopparmynt utan egentligt substansvärde 1715–19, konkurrens mellan riksgäldssedlar och Riksbankens sedlar 1789–1804, samt upphävandet av guldmyntfoten under första världskriget.2
Figur 1. Penningmängdstillväxt och inflation 1621–2021
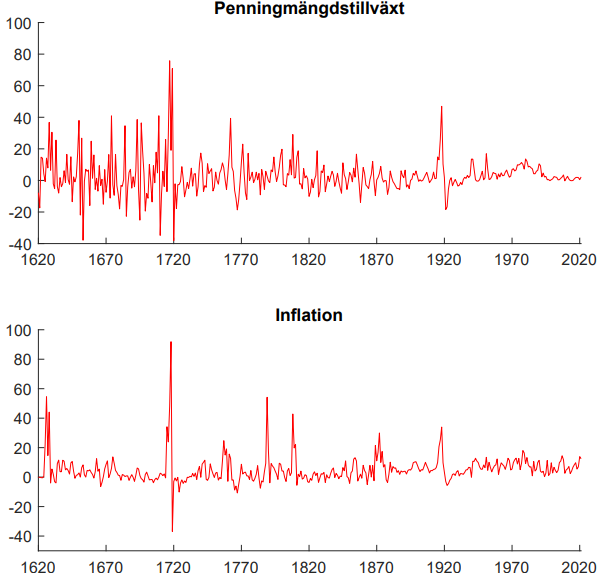
Anm: Båda variablerna ges i procent.
Källa: Edvinsson m fl (2025).
- Ekonometriskt ramverk
I vår empiriska analys använder vi VAR-modeller. Dessa beskriver det dynamiska sambandet mellan penningmängdstillväxt och inflation via ett bivariat ekvationssystem där tidigare värden på de två variablerna är de huvudsakliga förklaringsfaktorerna för dagens värden på dem. Modellerna skattas med bayesianska metoder utvecklade av Chan och Eisenstat (2018).3 I alla modeller tas det för givet att störningstermen har en specifik sorts tidsvarierande varians – s k stokastisk volatilitet. En tidsvarierande volatilitet förefaller som ett högst rimligt antagande givet hur data ser ut (figur 1) och är ett antagande som finner omfattande stöd i den empiriska makroekonomiska litteraturen; se t ex Cogley och Sargent (2005), Koop och Korobilis (2019) och Karlsson och Österholm (2021, 2023).
I ett första steg vill vi avgöra huruvida modellens dynamik är konstant eller tidsvarierande. I detta syfte skattas två modeller. Följande två specifikationer används i detta steg: 1) En modell med konstanta parametrar och 2) en modell med tidsvarierande parametrar. Tidsvariationen för parametrarna i den andra modellen är gradvis – den modelleras som s k slumpvandringar (random walks).4 I båda modellerna är inflationen endogen med avseende på penningmängdstillväxten, dvs tidigare värden på penningmängdstillväxten tillåts påverka inflationen.
När vi bestämt om modellens dynamik ska vara konstant eller tidsvarierande går vi i ett andra steg över till artikelns huvudfråga, nämligen om penningmängdstillväxten har prognosförmåga för inflationen. I detta andra steg skattar vi två versioner av den föredragna modellen. Om penningmängdstillväxten inte har prognosförmåga för inflationen innebär det att inflationen är exogen i VAR-modellen. Detta innebär att koefficienterna på tidigare värden av penningmängdstillväxten i ekvationen för inflationen är noll. Om penningmängdstillväxten däremot har prognosförmåga för inflationen är koefficienterna på tidigare värden av penningmängdstillväxten i ekvationen för inflationen nollskilda och vi säger att inflationen är endogen mot penningmängdstillväxten. De två modellerna karaktäriseras således av att inflationen är exogen i den ena modellen och endogen i den andra.
För att avgöra vilken modell som bäst beskriver data förlitar vi oss på måttet marginal likelihood när vi gör vår inomsampelanalys. Detta är ett mått som ofta används inom bayesiansk analys för att utvärdera hur väl modellen (och dess priors) överensstämmer med data; den modell som har högst marginal likelihood är bäst.
En modell med god anpassning inom samplet lyckas dock inte alltid göra bra prognoser.5 Därför undersöker vi också frågan om penningmängdstillväxtens prognosförmåga i en out-of-sample-analys. Detta görs på följande sätt: Vi utgår från resultaten i det första steget och skattar exogena och endogena modeller baserat på detta. Modellerna skattas först på samplet 1622 till 1671 och vi gör prognoser fyra år framåt, dvs för perioden 1672 till 1675. Samplet utökas därefter med en period (1622 till 1672), modellerna skattas om och nya prognoser fyra år framåt (1673 till 1676) görs. Detta pågår tills vi inte längre har några observationer kvar att utvärdera våra prognoser mot. Det sista samplet består således av perioden 1621 till 2020. Detta innebär att vi kan utvärdera 350 prognoser på ettårshorisonten, 349 på tvåårshorisonten, 348 på treårshorisonten och 347 på fyraårshorisonten.
Prognoserna utvärderas via sin prognosprecision. Denna mäts via det s k rotmedelkvadratfelet. Om modellen där penningmängden tillåts påverka inflationen har ett lägre rotmedelkvadratfel än modellen med exogen inflation tolkar vi detta som stöd för att penningmängden kan prognostisera inflationen. För att testa huruvida skillnaden i rotmedelkvadratfel är statistiskt signifikant används ett Diebold-Mariano-test (Diebold och Mariano 1995).6 För detaljer rörande modellspecifikation och övrig ekonometrisk analys, se Edvinsson m fl (2025).
- Resultat
Vi skattar inledningsvis modeller med konstanta och tidsvarierande parametrar där inflationen är endogen. Resultaten återfinns i tabell 1 och visar att modellen med tidsvarierande parametrar har högst marginal likelihood. Stödet för denna modell är, med Kass och Rafterys (1995) terminologi, ”mycket starkt” då två gånger skillnaden i log-marginal likelihood är 103,6.7
Tabell 1. Log-marginal likelihood för BVAR-modeller med olika antaganden rörande modellens dynamik

Anm: Modellerna har skattats på data från 1622–2021. I tabellen anges den naturliga logaritmen av marginal likelihood.
Källa: Edvinsson m fl (2025).
I ljuset av denna information går vi vidare och skattar modeller med tidsvarierande parametrar där inflationen antingen är endogen eller exogen med avseende på penningmängdstillväxten. Resultaten från denna övning återges i tabell 2.
Tabell 2. Log-marginal likelihood för BVAR-modeller med tidsvarierande parametrar och stokastisk volatilitet
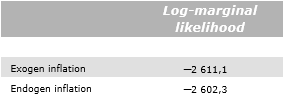
Anm: Modellerna har skattats på data från 1622–2021. I tabellen anges den naturliga logaritmen av marginal likelihood.
Källa: Edvinsson m fl (2025).
Som framgår av tabellen är modellen där inflationen är endogen den som föredras enligt marginal likelihood. Även här är stödet ”mycket starkt” då två gånger skillnaden i log–marginal likelihood är 17,6. Baserat på inomsampelanalysen drar vi således slutsatsen att penningmängdstillväxten har prognosförmåga för inflationen.
Hur ser då dynamiken ut i den föredragna modellen? Detta illustreras enklast genom modellens impuls-respons-funktioner, vilka beskriver den effekt som en störning till en variabel har på variablerna i systemet.8 I figur 2 visas effekten som en störning till penningmängdstillväxten av storleken en standardavvikelse har på penningmängdstillväxten. Noteras bör att denna standardavvikelse varierar över tiden eftersom modellen har stokastisk volatilitet. Storleken på störningen framgår av effekten på horisont noll. Som framgår av figuren har volatiliteten varit väldigt hög vid ett antal tillfällen – inte sällan i samband med krig. Mellan 1620 och 1624 tredubblades penningmängden i samband med att kopparmynt som innehöll mindre koppar än det nominella värdet präglades. Penningmängden femdubblades nästan mellan 1714 och 1718, bl a på grund av att s k nödmynt präglades. Och penningmängden fördubblades 1808 till 1809 i samband med att Riksbankssedlar inte längre kunde växlas in mot silver. Noteras kan dock att även om störningarna var mest volatila på 1710-talet så var effekterna på penningmängdstillväxten av dem mest långlivade på 1970-talet.
Figur 2. Impuls-respons-funktion: Effekt av en störning till penningmängdstillväxten på penningmängdstillväxten
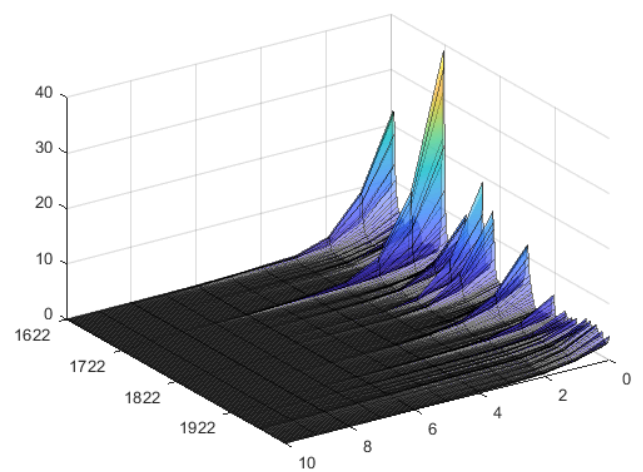
Anm: Modell med endogen inflation. Störningens storlek är en standardavvikelse. Procentenheter på vertikal axel. Horisont i kvartal samt tidpunkt på de horisontella axlarna.
Källa: Edvinsson m fl (2025).
Härnäst vänder vi blicken mot effekten på inflationen av störningar till penningmängdstillväxten. Denna återges i figur 3.9 I linje med vad som skulle kunna förväntas så ökar inflationen när penningmängdstillväxten är oväntat stark. Vi ser följaktligen stora effekter på inflationen i samband med de ovan utpekade perioderna. Av figuren framgår också att sambandet har förändrats över tiden. Störningarnas effekt på inflationen förefaller – liksom effekten på penningmängdstillväxten – ha varit mer långlivad på t ex 1970-talet än under den första halvan av den studerade perioden. En möjlig förklaring till detta är att ekonomin drevs mer av kortvariga utbudsstörningar (såsom misslyckade skördar) i det förindustriella samhället. Under 1970-talet kännetecknades svensk ekonomi i stället av en illa fungerande lönebildning med pris-löne-spiraler och en ekonomisk politik som var fokuserad på att hålla arbetslösheten låg snarare än vid jämviktsarbetslösheten. Detta ledde till en relativt hög och persistent inflation.
Figur 3. Impuls-respons-funktion: Effekt av en störning till penningmängdstillväxten på inflationen
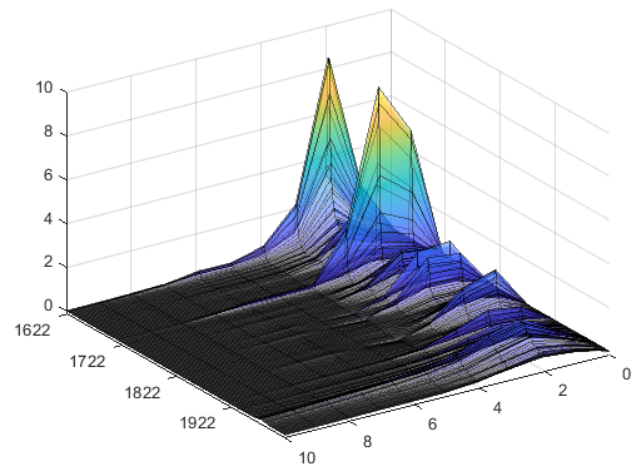
Anm: Modell med endogen inflation. Störningens storlek är en standardavvikelse. Procentenheter på vertikal axel. Horisont i kvartal samt tidpunkt på de horisontella axlarna.
Källa: Edvinsson m fl (2025).
Vår inomsampelanalys tyder alltså på att penningmängdstillväxten har prognosförmåga för inflationen. Detta kan jämföras med resultaten från vår out-of-sample-analys som återges i tabell 3.
Av tabellens översta rader framgår det att när hela samplet utvärderas har modellen där inflationen är endogen ett högre rotmedelkvadratfel än modellen där inflationen är exogen; detta är fallet oavsett vilken prognoshorisont vi tittar på. Skillnaderna är dock små. Den största skillnaden återfinns på tvåårshorisonten där modellen där inflationen är endogen har ett rotmedelkvadratfel som är fyra procent högre än modellen där inflationen är exogen; trots detta finner vi i två av fallen – på tre- och fyraårshorisonten – att skillnaden är statistiskt signifikant. Men det mest intressanta är naturligtvis att trots det mycket starka stöd för att penningmängdstillväxten har prognosförmåga för inflationen som vi fann i inomsampelanalysen ovan så finner vi här alltså stöd för att penningmängdstillväxten inte har prognosförmåga för inflationen.
För att undersöka detta resultat lite närmare så analyserar vi även rotmedelkvadratfelen för de ovan identifierade delperioderna 1672 till 1776, 1777 till 1873, 1874 till 1971 och 1972 till 2021. Resultaten från dessa är mer blandade. Som framgår av tabell 3 har modellen där inflationen är endogen det lägsta rotmedelkvadratfelet i sju fall: På fyraårshorisonten för perioden 1777 till 1873, på ett- och tvåårshorisonten för perioden 1874 till 1971 och på samtliga fyra horisonter för perioden 1972 till 2021. Av dessa erhålls dock en statistiskt signifikant skillnad enligt Diebold-Mariano-testet endast på tvåårshorisonten för perioden 1874 till 1971. I de övriga nio fallen har modellen där inflationen är exogen det lägsta rotmedelkvadratfelet. Skillnaden är dock statistiskt signifikant i endast tre av dessa fall.
Tabell 3. Rotmedelkvadratfel för olika perioder
| Period | Prognoshorisont (år) | Exogen inflation | Endogen inflation |
| 1672–2021 | 1 | 11,07 | 11,14 |
| 2 | 11,15 | 11,59 | |
| 3 | 11,12b | 11,33 | |
| 4 | 10,94a | 11,04 | |
| 1672–1776 | 1 | 18,00 | 18,15 |
| 2 | 17,63 | 18,62 | |
| 3 | 17,51b | 17,92 | |
| 4 | 17,05b | 17,22 | |
| 1777–1873 | 1 | 7,06 | 7,30 |
| 2 | 7,11 | 7,18 | |
| 3 | 7,15 | 7,15 | |
| 4 | 7,16 | 7,13 | |
| 1874–1971 | 1 | 6,25 | 5,99 |
| 2 | 7,44 | 7,25a | |
| 3 | 7,43 | 7,56 | |
| 4 | 7,48a | 7,62 | |
| 1972–2021 | 1 | 2,15 | 2,00 |
| 2 | 2,84 | 2,57 | |
| 3 | 3,13 | 2,93 | |
| 4 | 3,31 | 3,25 |
Anm: Rotmedelkvadratfel i procent. a och b indikerar signifikans för Diebold-Mariano-testet på en- respektive femprocentsnivån.
Källa: Författarnas beräkningar.
Sammanfattningsvis kan vi således notera att modellernas prognosförmåga out-of-sample på det stora hela förefaller vara ganska likartad även om den varierar något över tiden. Detta står i bjärt kontrast till resultaten i vår inomsampelanalys som gav ett mycket starkt stöd till modellen där inflationen är endogen mot penningmängdstillväxten. Motsägelsefulla resultat av denna typ är dock tyvärr inget ovanligt i den empiriska litteraturen. De exakta orsakerna bakom sådana resultat är oftast svåra att slå fast men en sannolik förklaring är s k overfitting, dvs att mer generöst parameteriserade modeller finner stöd vid inomsampelanalys men att denna generositet inte genererar någon förbättring i prognosförmåga out-of-sample.
Det är dock avslutningsvis värt att påpeka att det faktum att modellen där inflationen är endogen inte lyckades göra bättre prognoser än modellen där den är exogen inte innebär att penningmängdstillväxten inte spelar någon roll för inflationen. Vår analys har ju fokuserat på det intertemporala sambandet mellan penningmängdstillväxt och inflation, men det finns ju även ett kontemporärt samband.
Ovan har det kontemporära sambandet mellan variablerna antagits vara sådant att inflationen kan påverka penningmängdstillväxten; penningmängdstillväxten kan dock inte påverka inflationen kontemporärt – detta kan endast ske med en fördröjning (dvs tidigast efter ett år). Anledningen till detta är den rekursiva identifikationsstruktur som modellen har.
För att få en uppfattning om hur det kontemporära sambandet ser ut mellan variablerna om vi släpper på det ovan nämnda identifierande antagandet visas i figur 4 den skattade, tidsvarierande korrelationen mellan residualerna från VAR-modellens reducerade form.10
Figur 4. Skattad korrelation mellan störningar till inflation och penningmängdstillväxt i reducerad form
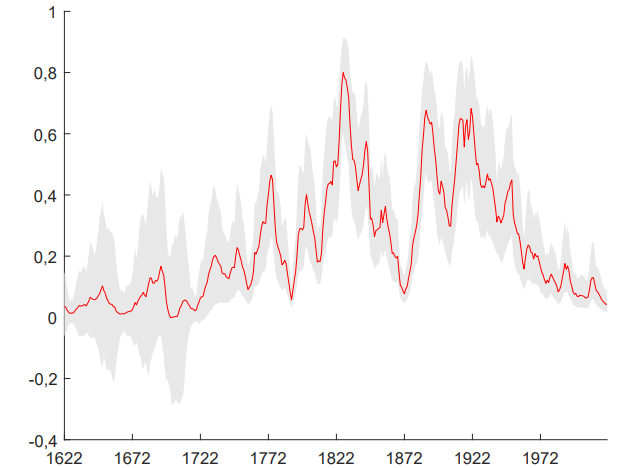
Anm: Modell med endogen inflation. Grå band ger 68-procentiga trovärdiga intervall (bayesianska konfidensintervall).
Källa: Edvinsson m fl (2025).
Av figuren framgår att det typiskt sett är en positiv korrelation mellan residualerna. Korrelationens storlek varierar; från 1622 till mitten på 1700-talet och i slutet på den studerade perioden är korrelationen låg. Relativt höga värden – större än 0,6 – återfinns på 1820-talet, i slutet av 1800-talet och i samband med första världskriget. Några kausala slutsatser kan inte dras utifrån detta, men vi noterar att en positiv korrelation är konsistent med att hög penningmängdstillväxt genererar hög inflation samma år. Å andra sidan är en positiv korrelation naturligtvis också konsistent med att hög inflation genererar hög penningmängdstillväxt samma år. Vår sammanfattande slutsats blir således att penningmängdstillväxten sannolikt påverkar inflationen – åtminstone kontemporärt – men att vår out-of-sample-analys ifrågasätter huruvida penningmängdstillväxten kan prognostisera inflationen.
- Avslutande kommentarer
I denna artikel har vi analyserat huruvida penningmängdstillväxt kan prognostisera inflation i Sverige. Detta har gjorts på ett datamaterial som sträcker sig från 1620 till 2021.
Vår inomsampelanalys indikerar tydligt att sambandet mellan penningmängdstillväxt och inflation är tidsvarierande – en slutsats som också är i linje med forskning med ett mer samtida fokus; se t ex Berger och Österholm (2011a, 2011b), Berger m fl (2023) och Borio m fl (2023). Den indikerar också att penningmängdstillväxten har prognosförmåga för inflationen. Detta återspeglas dock inte i vår out-of-sample-analys där prognosprecisionen för inflationen inte förbättras när penningmängdstillväxten beaktas.
Vi noterar slutligen att det typiskt sett finns ett positivt kontemporärt samband mellan de två variablerna. Detta innebär att även om vår out-of-sample-analys ifrågasätter huruvida det finns några dynamiska effekter från penningmängdstillväxten på inflationen så kan det inte uteslutas att penningmängdstillväxten ändå påverkar inflationen.
1 Det kan även noteras att Jonung (1976) studerade sambandet mellan penningmängdstillväxt och inflation i Sverige under perioden 1732–1972.
2 För en beskrivning av episoden med konkurrens mellan riksgäldssedlar och Riksbankens sedlar, se Stein (2025).
3 Bayesianska metoder kan förenklat beskrivas som att analysen kombinerar den information som datamaterialet innehåller med förhandsinformation – s k priors – som forskaren har.
4 I båda modellerna sätts laglängden till två.
5 Se t ex Clark (2004), Inoue and Kilian (2004) och Rossi and Sekhposyan (2011).
6 Detta test är strikt sett inte gjort för jämförelser av prognoser genererade på detta sätt. I frånvaro av test framtagna för detta syfte använder vi dock – i linje med Diebolds (2015) rekommendation – testet eftersom mycket talar för att det fungerar relativt väl.
7 Det kan noteras att gränsen för ”mycket starkt” – som är den högsta kategorin – går vid tio.
8 Impuls-respons-funktionerna baseras på en rekursiv identifikation som innebär att inflationen kan påverka penningmängdstillväxten kontemporärt, men att penningmängdstillväxten kan påverka inflationen först med en periods fördröjning.
9 Modellens resterande impuls-respons-funktioner återfinns i figur 5 och figur 6 i i Edvinsson m fl (2025).
10 Förenklat kan den reducerade formen beskrivas som en specifikation där residualerna från de två ekvationerna tillåts samvariera. I den strukturella form som modellen ursprungligen skattas är residualerna okorrelerade med varandra. Se Edvinsson m fl (2025), särskilt fotnot 6, för detaljer.
Berger, H, S Karlsson och P Österholm (2023), ”A Note of Caution on the Relation between Money Growth and Inflation”, Scottish Journal of Political Economy, vol 70, s 479–496.
Berger, H och P Österholm (2011a), ”Does Money Granger Cause Inflation in the Euro Area? Evidence from Out-of-Sample Forecasts Using Bayesian VARs”, Economic Record, vol 87, s 45–60.
Berger, H och P Österholm. (2011b), ”Does Money Matter for U.S. Inflation? Evidence from Bayesian VARs”, CESifo Economic Studies, vol 57, s 531–550.
Borio, C, B Hofmann och E Zakrajšek (2023), ”Does Money Growth Help Explain the Recent Inflation Surge?”, BIS Bulletin 67, Basel.
Chan, J C C och E Eisenstat (2018), ”Comparing Hybrid Time-varying Parameter VARs”, Economics Letters, vol 171, s 1–5.
Clark, T E (2004), ”Can Out-of-Sample Forecast Comparisons Help Prevent Overfitting?”, Journal of Forecasting, vol 23, s 115–139.
Cogley, T och T J Sargent (2005), ”Drifts and Volatilities: Monetary Policies and Outcomes in the Post WWII US”, Review of Economic Dynamics, vol 8, s 262–302.
Diebold, F X (2015), ”Comparing Predictive Accuracy, Twenty Years Later: A Personal Perspective on the Use and Abuse of Diebold-Mariano Tests”, Journal of Business and Economic Statistics, vol 33, s 1–9.
Diebold, F X och R S Mariano (1995), ”Comparing Predictive Accuracy”, Journal of Business and Economic Statistics, vol 13, s 253–263.
Edvinsson, R, S Karlsson och P Österholm (2025), ”Does Money Growth Predict Inflation in Sweden? Evidence from Vector Autoregressions Using Four Centuries of Data”, Empirical Economics, vol 68, s 1613–1635.
Edvinsson, R och J Söderberg (2010), ”The Evolution of Swedish Consumer Prices 1290-2008”, i Edvinsson, R, T Jacobson och D Waldenström (red), Historical Monetary and Financial Statistics for Sweden: Exchange Rates, Prices and Wages 1277–2008, Sveriges Riksbank och Ekerlids, Stockholm.
Edvinsson, R och J Söderberg (2011), ”A Consumer Price Index for Sweden 1290–2008”, Review of Income and Wealth, vol 57, s 270–292.
Edvinsson, R och A Ögren (2014), ”Swedish Money Supply, 1620–2012”, i Edvinsson, R, T Jacobson och D Waldenström (red), Historical Monetary and Financial Statistics for Sweden, vol. 2: House Prices, Stock Returns, National Accounts and the Riksbank Balance Sheet 1620–2012, Sveriges Riksbank och Ekerlids, Stockholm.
Europeiska Centralbanken (2021), ”An Overview of the ECB’s Monetary Policy Strategy”, ECB Economic Bulletin, vol 5/2021, s 75–89.
Golez, B och P Koudjis (2018), ”Four Centuries of Return Predictability”, Journal of Financial Economics, vol 127, s 248–263.
Harvey, D I, N M Kellard, J B Madsen och M E Wohar (2010), ”The Prebisch-Singer Hypothesis: Four Centuries of Evidence”, Review of Economics and Statistics, vol 92, s 367–377.
Inoue, A och L Kilian (2004), ”In-Sample or Out-of-Sample Tests of Predictability: Which One Should We Use?”, Econometric Reviews, vol 23, s 371–402.
Jonung, L (1976), ”Money and Prices in Sweden 1732-1972”, Scandinavian Journal of Economics, vol 78, s 40–58.
Karlsson, S och P Österholm (2021), ”Okuns lag i Sverige – är sambandet stabilt?”, Ekonomisk Debatt, vol 49, nr 8, s 39–47.
Karlsson, S och P Österholm (2023), ”Is the US Phillips Curve Stable? Evidence from Bayesian VARs”, Scandinavian Journal of Economics, vol 125, s 287–314.
Kass, R E och A E Raftery (1995), ”Bayes Factors”, Journal of the American Statistical Association, vol 90, s 773–795.
Koop, G och D Korobilis (2019), ”Forecasting with High-dimensional Panel VARs”, Oxford Bulletin of Economics and Statistics, vol 81, s 937–-959.
Plakandaras, V, R Gupta och M Wohar (2023), ”Are Real Interest Rates a Monetary Phenomenon? Evidence from over 700 Years of Data”, Research in International Business and Finance, vol 66, 102010.
Rossi, B och T Sekhposyan (2011), ”Understanding Models’ Forecasting Performance”, Journal of Econometrics, vol 164, s 158–172.
Stein, G (2025), ”En valuta – två värden”, Ekonomisk Debatt, vol 53, nr 6, s 46–51.
Verdickt, G, J Annaert och M Deloof (2019), ”Dividend Growth and Return Predictability: A Long-run Re-Examination of Conventional Wisdom”, Journal of Empirical Finance, vol 52, s 112–127.
Woodford, M (2008), ”How Important is Money in the Conduct of Monetary Policy?”, Journal of Money, Credit and Banking, vol 40, s 1551–1598.